Table of Contents
अध्याय 8
चतुर्भुज
8.1 भूमिका
आप अध्यायों 6 और 7 में त्रिभुजों के अनेक गुणों के बारे में अध्ययन कर चुके हैं। आप यह भी जानते हैं कि तीन असंरेख बिंदुओं को युग्मों में जोड़ने पर जो आकृति प्राप्त होती है, त्रिभुज कहलाती है। अब, आइए चार बिंदु अंकित करें और देखें कि क्रमानुसार युग्मों में इनको जोड़ने पर क्या आकृति प्राप्त होती है।
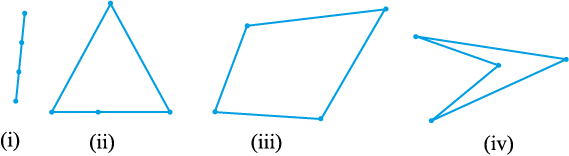
आकृति 8.1
ध्यान दीजिए कि यदि सभी बिंदु संरेख हों (एक ही रेखा में हों), तो हमें एक रेखाखंड प्राप्त होता है [ देखिए आकृति 8.1 (i)]। यदि चार बिंदुओं में से तीन संरेख हों, तो हमें एक त्रिभुज प्राप्त होता है [देखिए आकृति 8.1 (ii)] और यदि चार में से कोई तीन बिंदु संरेख न हों, तो हमें चार भुजाओं वाली एक आकृति प्राप्त होती है [देखिए आकृति 8.1 (iii) और (iv)]।
चारों बिन्दुओं को एक क्रम में जोड़ने से इस प्रकार प्राप्त आकृति चतुर्भुज (quadrilateral) कहलाती है। इस पुस्तक में हम केवल आकृति 8.1 (iii) में दिए गए जैसे चतुर्भुजों का ही अध्ययन करेंगे और आकृति 8.1 (iv) में दिए गए जैसे चतुर्भुजों का नहीं।
एक चतुर्भुज की चार भुजाएँ, चार कोण और चार शीर्ष होते हैं [ देखिए आकृति 8.2 (i)]।
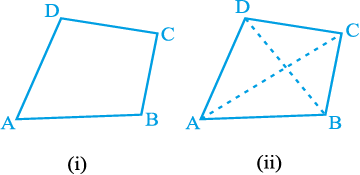
आकृति 8.2
चतुर्भुज ABCD में, AB, BC, CD और DA चार भुजाएँ हैं; A, B, C और D चार शीर्ष हैं तथा ∠ A, ∠ B, ∠ C और ∠ D शीर्षों पर बने चार कोण हैं।
अब सम्मुख शीर्षों A और C तथा B और D को जोड़िए [देखिए आकृति 8.2 (ii)]।
AC और BD चतुर्भुज ABCD के दो विकर्ण (diagonals) कहलाते हैं।
इस अध्याय में, हम विभिन्न प्रकार के चतुर्भुजों और उनके गुणों के बारे में अध्ययन करेंगे। विशेष तौर पर हम समांतर चतुर्भुजों के बारे में पढ़ेंगे।
आप सोच सकते हैं कि हम चतुर्भुजों (या समांतर चतुर्भुजों) का क्यों अध्ययन करें। अपने परिवेश में देखिए। आप अपने आस-पास चतुर्भुज के आकार की अनेक वस्तुएँ देख सकते हैं, जैसे- आपकी कक्षा का फर्श, दीवार, छत, खिड़कियाँ, श्यामपट्ट, डस्टर (duster) का प्रत्येक फलक, आपकी पुस्तक का प्रत्येक पृष्ठ, पढ़ने की मेज का ऊपरी पृष्ठ, इत्यादि। इनमें से कुछ को नीचे दिखाया गया है (देखिए आकृति 8.3)।

आकृति 8.3
यद्यपि हमारे आस-पास दिखने वाली अधिकांश वस्तुएँ आयत के आकार की हैं, फिर भी हम चतुर्भुजों और विशेषकर समांतर चतुर्भुजों के बारे में और अधिक अध्ययन करेंगे, क्योंकि एक आयत एक समांतर चतुर्भुज ही है और समांतर चतुर्भुज के सभी गुण आयत के लिए भी सत्य होते हैं।
8.2 चतुर्भुज का कोण योग गुण
अब, आइए एक चतुर्भुज के कोण योग गुण का पुनर्विलोकन करें।
चतुर्भुज के कोणों का योग 3600 होता है। हम इसकी जाँच चतुर्भुज का एक विकर्ण खींच कर उसे दो त्रिभुजों में विभाजित करके कर सकते हैं।
मान लीजिए ABCD एक चतुर्भुज है और AC उसका एक विकर्ण है (देखिए आकृति 8.4)।
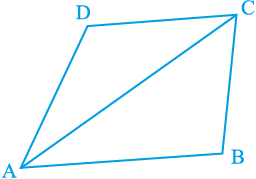
आकृति 8.4
∆ ADC के कोणों का क्या योग है?
हम जानते हैं कि
∠ DAC + ∠ ACD + ∠ D = 180° (1)
इसी प्रकार, ∆ ABC में,
∠ CAB + ∠ ACB + ∠ B = 180° (2)
(1) और (2) को जोड़ने पर, हमें प्राप्त होता है:
∠ DAC + ∠ ACD + ∠ D + ∠ CAB + ∠ ACB + ∠ B = 180° + 180° = 360°
साथ ही, ∠ DAC + ∠ CAB = ∠ A और ∠ ACD + ∠ ACB = ∠ C
अत:, ∠ A + ∠ D + ∠ B + ∠ C = 360° है।
अर्थात् चतुर्भुज के कोणों का योग 360° होता है।
8.3 चतुर्भुज के प्रकार
नीचे दिए गए विभिन्न चतुर्भुजों को देखिए :
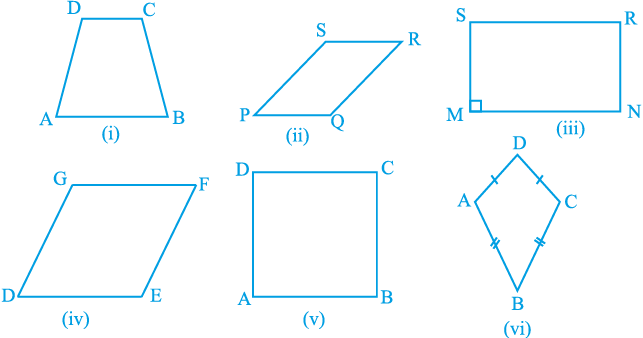
आकृति 8.5
ध्यान दीजिए कि :
• आकृति 8.5 (i) में, चतुर्भुज ABCD की सम्मुख भुजाओं AB और CD का एक युग्म समांतर है। आप जानते हैं कि यह एक समलंब (trapezium) कहलाता है।
• आकृतियों 8.5 (ii), (iii) , (iv) और (v) में दिए सभी चतुर्भुजों में सम्मुख भुजाओं के दोनों युग्म समांतर हैं। ये चतुर्भुज समांतर चतुर्भुज (parallelograms) कहलाते हैं। अत:, आकृति 8.5 (ii) का चतुर्भुज PQRS एक समांतर चतुर्भुज है। इसी प्रकार, आकृतियों 8.5 (iii), (iv) और (v) में दिए सभी चतुर्भुज समांतर चतुर्भुज हैं।
• ध्यान दीजिए कि आकृति 8.5 (iii) के समांतर चतुर्भुज MNRS में एक कोण M समकोण है। यह विशेष समांतर चतुर्भुज क्या कहलाता है? याद कीजिए, यह एक आयत (rectangle) कहलाता है।
• आकृति 8.5 (iv) में दिए समांतर चतुर्भुज DEFG की सभी भुजाएँ बराबर हैं और हम जानते हैं कि यह एक समचतुर्भुज (rhombus) कहलाता है।
• आकृति 8.5 (v) के समांतर चतुर्भुज ABCD में, ∠ A = 90° और सभी भुजाएँ बराबर हैं। यह एक वर्ग (square) कहलाता है।
• आकृति 8.5 (vi) के चतुर्भुज ABCD में, AD = CD और AB = CB है, अर्थात् आसन्न भुजाओं के दो युग्म बराबर हैं। यह एक समांतर चतुर्भुज नहीं है। यह एक पतंग (kite) कहलाता है।
ध्यान दीजिए कि वर्ग, आयत और समचतुर्भुज में से प्रत्येक एक समांतर चतुर्भुज होता है।
• एक वर्ग एक आयत है और एक समचतुर्भुज भी है।
• एक समांतर चतुर्भुज एक समलंब है।
• पतंग एक समांतर चतुर्भुज नहीं है।
• समलंब एक समांतर चतुर्भुज नहीं है (क्योंकि इसमें सम्मुख भुजाओं का एक युग्म ही समांतर है और समांतर चतुर्भुज के लिए सम्मुख भुजाओं के दोनों युग्म समांतर होने चाहिए)।
• एक आयत अथवा एक समचतुर्भुज एक वर्ग नहीं है।
आकृति 8.6 को देखिए। इसमें समान परिमाप 14 cm वाला एक आयत और एक समांतर चतुर्भुज दिया है।
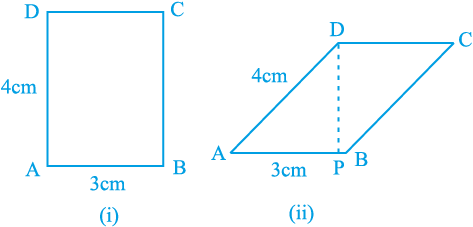
आकृति 8.6
यहाँ समांतर चतुर्भुज का क्षेत्रफल DP × AB है और यह आयत के क्षेत्रफल AB × AD से कम है, क्योंकि DP < AD है। सामान्यत:, मिठाई के दुकानदार ‘बरफी’ को समांतर चतुर्भुज के आकार में काटते हैं, ताकि एक ही ट्रे (परात) में बरफी के अधिक टुकड़े आ सकें (अगली बार जब आप बरफी खाएँ, तो उसका आकार देख लें)।
आइए अब पिछली कक्षाओं में पढ़े हुए समांतर चतुर्भुजों के कुछ गुणों का पुनर्विलोकन करें।
8.4 समांतर चतुर्भुज के गुण
आइए एक क्रियाकलाप करें।
कागज पर एक समांतर चतुर्भुज खींच कर उसे काट लीजिए। अब इसे विकर्ण के अनुदिश काट लीजिए (देखिए आकृति 8.7)। आप दो त्रिभुज प्राप्त करते हैं। इन त्रिभुजों के बारे में आप क्या कह सकते हैं?
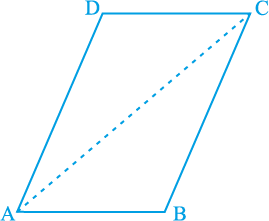
आकृति 8.7
एक त्रिभुज को दूसरे त्रिभुज पर रखिए। यदि आवश्यक हो, तो त्रिभुज को घुमाइए भी। आप क्या देखते हैं?
देखिए कि दोनों त्रिभुज परस्पर सर्वांगसम हैं।
कुछ और समांतर चतुर्भुज खींच कर इस क्रियाकलाप को दोहराइए। प्रत्येक बार आप पाएँगे कि समांतर चतुर्भुज का एक विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभाजित करता है।
अब आइए इस परिणाम को सिद्ध करें।
प्रमेय 8.1 : किसी समांतर चतुर्भुज का एक विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभाजित करता है।
उपपत्ति : मान लीजिए ABCD एक समांतर चतुर्भुज है और AC उसका एक विकर्ण है (देखिए आकृति 8.8)। देखिए कि विकर्ण AC समांतर चतुर्भुज ABCD को दो त्रिभुजों ABC और CDA में विभाजित करता है। हमें सिद्ध करना है कि ये दोनों त्रिभुज सर्वांगसम हैं।
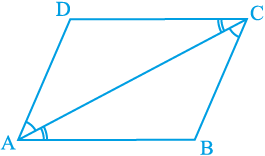
आकृति 8.8
∆ ABC और ∆ CDA के लिए ध्यान दीजिए कि BC || AD है और AC एक तिर्यक रेखा है।
इसलिए, ∠ BCA = ∠ DAC (एकांतर कोणों का युग्म)
साथ ही, AB || DC और AC एक तिर्यक रेखा है।
इसलिए, ∠ BAC = ∠ DCA (एकांतर कोणों का युग्म)
और AC = CA (उभयनिष्ठ)
अत:, ∆ ABC ≅ ∆ CDA (ASA नियम)
अर्थात् विकर्ण AC समांतर चतुर्भुज ABCD को दो सर्वांगसम त्रिभुजों ABC और CDA में विभाजित करता है।
अब समांतर चतुर्भुज ABCD की सम्मुख भुजाओं को मापिए। आप क्या देखते हैं?
आप पाएँगे कि AB = DC और AD = BC है।
यह समांतर चतुर्भुज का एक अन्य गुण है, जिसे नीचे दिया जा रहा है:
प्रमेय 8.2 : एक समांतर चतुर्भुज में सम्मुख भुजाएँ बराबर होती हैं।
आप पहले ही सिद्ध कर चुके हैं कि समांतर चतुर्भुज का विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभाजित करता है। अत:, आप इनके संगत भागों, मान लीजिए भुजाओं, के बारे में क्या कह सकते हैं? ये बराबर हैं।
इसलिए, AB = DC और AD = BC है।
अब इस परिणाम का विलोम क्या है? आप जानते हैं कि जो प्रमेय (किसी कथन) में दिया हो, तो उसके विलोम में उसे सिद्ध करना होता है और जो प्रमेय में दिया गया है उसे विलोम में दिया हुआ माना जाता है। ध्यान दीजिए कि प्रमेय 8.2 को निम्न रूप में भी लिखा जा सकता है:
यदि एक चतुर्भुज एक समांतर चतुर्भुज है, तो उसकी सम्मुख भुजाओं का प्रत्येक युग्म बराबर होता है। इसलिए, इसका विलोम निम्न होगा:
प्रमेय 8.3 : यदि एक चतुर्भुज की सम्मुख भुजाओं का प्रत्येक युग्म बराबर हो, तो वह एक समांतर चतुर्भुज होता है।
क्या आप इसके कारण दे सकते हैं?
मान लीजिए चतुर्भुज ABCD की भुजाएँ AB और CD बराबर हैं और साथ ही AD = BC है (देखिए आकृति 8.9)। विकर्ण AC खींचिए।
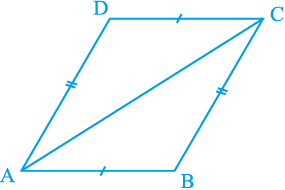
आकृति 8.9
स्पष्टत:, ∆ ABC ≅ ∆ CDA (क्यों?)
अत:, ∠ BAC = ∠ DCA
और ∠ BCA = ∠ DAC (क्यों?)
क्या अब आप कह सकते हैं कि ABCD एक समांतर चतुर्भुज है? (क्यों?)
आपने अभी देखा है कि एक समांतर चतुर्भुज में सम्मुख भुजाओं का प्रत्येक युग्म बराबर होता है और विलोमत: यदि किसी चतुर्भुज में सम्मुख भुजाओं का प्रत्येक युग्म बराबर हो, तो वह एक समांतर चतुर्भुज होता है। क्या हम यही परिणाम सम्मुख कोणों के युग्मों के बारे में भी निकाल सकते हैं?
एक समांतर चतुर्भुज खींचिए और उसके कोणों को मापिए। आप क्या देखते हैं?
सम्मुख कोणों का प्रत्येक युग्म बराबर है।
इसे कुछ और समांतर चतुर्भुज लेकर दोहराइए। इससे हम एक अन्य परिणाम पर पहुँचते हैं, जो निम्न है:
प्रमेय 8.4 : एक समांतर चतुर्भुज में सम्मुख कोण बराबर होते हैं।
अब, क्या इस परिणाम का विलोम भी सत्य है? हाँ, एेसा ही है। चतुर्भुज के कोण योग गुण और तिर्यक रेखा द्वारा प्रतिच्छेदित समांतर रेखाओं के गुणों का प्रयोग करके, हम देख सकते हैं कि उपरोक्त का विलोम भी सत्य है। इस प्रकार, हमें निम्न प्रमेय प्राप्त होती है:
प्रमेय 8.5 : यदि एक चतुर्भुज में सम्मुख कोणों का प्रत्येक युग्म बराबर हो, तो वह एक समांतर चतुर्भुज होता है।
समांतर चतुर्भुज का एक गुण और भी है। आइए इसका अध्ययन करें। एक समांतर चतुर्भुज ABCD खींचिए और उसके दोनों विकर्ण AC और BD खींचिए, जो परस्पर O पर प्रतिच्छेद करते हैं (देखिए आकृति 8.10)।
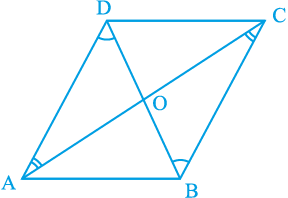
आकृति 8.10
OA, OB, OC और OD की लम्बाइयाँ मापिए।
आप क्या देखते हैं? आप देखेंगे कि
OA = OC और OB = OD
है। अर्थात् O दोनों विकर्णों का मध्य-बिंदु है।
कुछ और समांतर चतुर्भुज लेकर इस क्रियाकलाप को दोहराइए।
प्रत्येक बार, आप प्राप्त करेंगे कि O दोनों विकर्णों का मध्य-बिंदु है।
इस प्रकार, हम निम्न प्रमेय प्राप्त करते हैं:
प्रमेय 8.6 : समांतर चतुर्भुज के विकर्ण एक दूसरे को (परस्पर) समद्विभाजित करते हैं।
अब, यदि एक चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करें, तो क्या होगा? क्या यह एक समांतर चतुर्भुज होगा? वास्तव में, यह सत्य है।
यह प्रमेय 8.6 के परिणाम का विलोम है। इसे नीचे दिया जा रहा है:
प्रमेय 8.7 : यदि एक चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करें, तो वह एक समांतर चतुर्भुज होता है।
आप इस परिणाम के लिए तर्क निम्न प्रकार दे सकते हैं:
ध्यान दीजिए कि आकृति 8.11 में, यह दिया है कि OA = OC और OB = OD है।
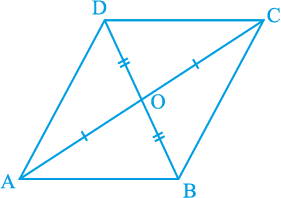
आकृति 8.11
अत:, ∆ AOB ≅ ∆ COD (क्यों?)
इसलिए, ∠ ABO = ∠ CDO (क्यों?)
इससे हमें AB || CD प्राप्त होता है।
इसी प्रकार, BC || AD है।
अत:, ABCD एक समांतर चतुर्भुज है।
आइए अब कुछ उदाहरण लें।
उदाहरण 1 : दर्शाइए कि एक आयत का प्रत्येक कोण एक समकोण होता है।
हल : याद कीजिए कि एक आयत क्या होता है।
एक आयत वह समांतर चतुर्भुज होता है जिसका एक कोण समकोण हो।
मान लीजिए ABCD एक आयत है, जिसमें ∠ A = 90° है।
हमें दर्शाना है कि ∠ B = ∠ C = ∠ D = 90° है।
AD || BC और AB एक तिर्यक रेखा है (देखिए आकृति 8.12)।

आकृति 8.12
इसलिए, ∠ A + ∠ B = 180° (तिर्यक रेखा के एक ही ओर के अंत: कोण)
परन्तु, ∠ A = 90° है।
इसलिए, ∠ B = 180° – ∠ A = 180° – 90° = 90°
अब ∠ C = ∠ A और ∠ D = ∠ B (समांतर चतुर्भुज के सम्मुख कोण)
इसलिए, ∠ C = 90° और ∠ D = 90°
अत:, आयत का प्रत्येक कोण 900 है।
उदाहरण 2 : दर्शाइए कि एक समचतुर्भुज के विकर्ण परस्पर लम्ब होते हैं।
हल : समचतुर्भुज ABCD पर विचार कीजिए (देखिए आकृति 8.13)।
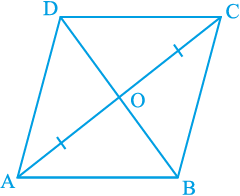
आप जानते हैं कि AB = BC = CD = DA (क्यों?)
अब, ∆ AOD और ∆ COD में,
OA = OC (समांतर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं)
OD = OD (उभयनिष्ठ)
AD = CD (दिया है)
अत:, ∆ AOD ≅ ∆ COD (SSS सर्वांगसमता नियम)
इसलिए, ∠ AOD = ∠ COD (CPCT)
परन्तु, ∠ AOD + ∠ COD = 180° (रैखिक युग्म)
इसलिए, 2∠ AOD = 180°
या, ∠ AOD = 90°
अत:, समचर्तुभुज के विकर्ण परस्पर लम्ब हैं।
उदाहरण 3 : ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है। AD बहिष्कोण PAC को समद्विभाजित करता है और CD || BA है (देखिए आकृति 8.14)। दर्शाइए कि
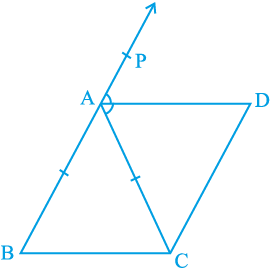
आकृति 8.14
(i) ∠ DAC = ∠ BCA और (ii) ABCD एक समांतर चतुर्भुज है।
हल : (i) ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है। (दिया है)
इसलिए, ∠ ABC = ∠ ACB (बराबर भुजाओं के सम्मुख कोण)
साथ ही, ∠ PAC = ∠ ABC + ∠ ACB
(त्रिभुज का बहिष्कोण)
या, ∠ PAC = 2∠ ACB (1)
अब, AD कोण PAC को समद्विभाजित करती है।
इसलिए, ∠ PAC = 2∠ DAC (2)
अत:,
2∠ DAC = 2∠ ACB [(1) और (2) से]
या, ∠ DAC = ∠ ACB
(ii) अब ये दोनों बराबर कोण वे एकांतर कोण हैं जो रेखाखंडों BC और AD को तिर्यक रेखा AC द्वारा प्रतिच्छेद करने से बनते हैं।
इसलिए, BC || AD
साथ ही, BA || CD है।
इस प्रकार, चतुर्भुज ABCD की सम्मुख भुजाओं के दोनों युग्म समांतर हैं।
अत:, ABCD एक समांतर चतुर्भुज है।
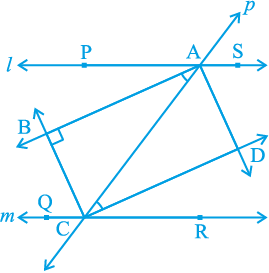
उदाहरण 4 : दो समांतर रेखाओं l और m को एक तिर्यक रेखा p प्रतिच्छेद करती है (देखिए आकृति 8.15)। दर्शाइए कि अंत: कोणों के समद्विभाजकों से बना चतुर्भुज एक आयत है।
आकृति 8.15
हल : यह दिया है कि l || m है और तिर्यक रेखा p इन्हें क्रमश: बिंदुओं A और C पर प्रतिच्छेद करती है।
∠ PAC और ∠ ACQ के समद्विभाजक B पर प्रतिच्छेद करते हैं और ∠ ACR और ∠ SAC के समद्विभाजक D पर प्रतिच्छेद करते हैं।
हमें दर्शाना है कि चतुर्भुज ABCD एक आयत है।
अब, ∠ PAC = ∠ ACR
(l || m और तिर्यक रेखा p से बने एकांतर कोण)
इसलिए, 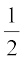 ∠ PAC =
∠ PAC = 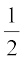 ∠ ACR
∠ ACR
अर्थात्, ∠ BAC = ∠ ACD
ये बराबर कोण रेखाओं AB और DC के तिर्यक रेखा AC द्वारा प्रतिच्छेदित करने से बनते हैं और ये एकांतर कोण हैं।
इसलिए, AB || DC
इसी प्रकार, BC || AD (∠ ACB और ∠ CAD लेने पर)
अत:, ABCD एक समांतर चतुर्भुज है।
साथ ही, ∠ PAC + ∠ CAS = 180° (रैखिक युग्म)
इसलिए, 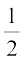 ∠ PAC +
∠ PAC +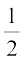 ∠ CAS =
∠ CAS = 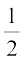 × 180° = 90°
× 180° = 90°
या, ∠ BAC + ∠ CAD = 90°
या, ∠ BAD = 90°
इसलिए, ABCD एक समांतर चतुर्भुज है जिसका एक कोण समकोण है।
अत: ABCD एक आयत है।
उदाहरण 5 : दर्शाइए कि एक समांतर चतुर्भुज के कोणों के समद्विभाजक एक आयत बनाते हैं।
हल : मान लीजिए P, Q, R और S क्रमश: समांतर चतुर्भुज ABCD के ∠ A और ∠ B, ∠ B और ∠ C, ∠ C और ∠ D तथा ∠ D और ∠ A के समद्विभाजकों के प्रतिच्छेद बिंदु हैं (देखिए आकृति 8.16)।
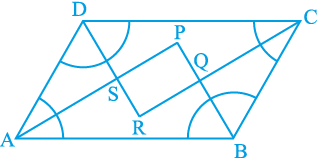
आकृति 8.16
∆ ASD में आप क्या देख सकते हैं?
चूँकि DS कोण D को और AS कोण A को समद्विभाजित करते हैं, इसलिए
∠ DAS + ∠ ADS = 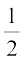 ∠ A +
∠ A + 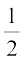 ∠ D
∠ D
= 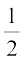 (∠ A + ∠ D)
(∠ A + ∠ D)
= 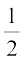 × 180°
× 180°
(∠ A और ∠ D तिर्यक रेखा के एक ही ओर के अंत: कोण हैं)
= 90°
साथ ही, ∠ DAS + ∠ ADS + ∠ DSA = 180° (त्रिभुज का कोण योग गुण)
या, 90° + ∠ DSA = 180°
या, ∠ DSA = 90°
अत:, ∠ PSR = 90° (∠ DSA का शीर्षाभिमुख कोण)
इसी प्रकार, यह दर्शाया जा सकता है कि ∠ APB = 90° या ∠ SPQ = 90° (जैसा कि ∠ DSA के लिए किया था)। इसी प्रकार, ∠ PQR = 90° और ∠ SRQ = 90° है।
इसलिए, PQRS एक एेसा चतुर्भुज है जिसके सभी कोण समकोण हैं।
क्या हम निष्कर्ष निकाल सकते हैं कि यह एक आयत है? आइए इसकी जाँच करें।
हम दर्शा चुके हैं कि∠ PSR = ∠ PQR = 90° और ∠ SPQ = ∠ SRQ = 90° है, अर्थात् सम्मुख कोणों के दोनों युग्म बराबर हैं।
अत: PQRS एक समांतर चतुर्भुज है, जिसमें एक कोण (वास्तव में सभी कोण) समकोण हैं। इसलिए, PQRS एक आयत है।
8.5 चतुर्भुज के समांतर चतुर्भुज होने के लिए एक अन्य प्रतिबन्ध
इस अध्याय में, आपने समांतर चतुर्भुजों के अनेक गुणों का अध्ययन किया है और आपने यह भी जाँच की है कि यदि एक चतुर्भुज इन गुणों में से किसी एक गुण को भी संतुष्ट करे, तो वह एक समांतर चतुर्भुज होता है।
अब हम एक और प्रतिबन्ध का अध्ययन करेंगे, जो एक चतुर्भुज के समांतर चतुर्भुज होने के लिए न्यूनतम प्रतिबन्ध है।
इसे एक प्रमेय के रूप में नीचे दिया जा रहा है:
प्रमेय 8.8 : कोई चतुर्भुज एक समांतर चतुर्भुज होता है, यदि उसकी सम्मुख भुजाओं का एक युग्म बराबर हो और समांतर हो।
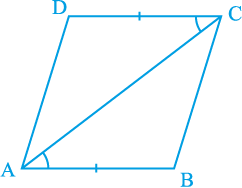
आकृति 8.17
आकृति 8.17 को देखिए, जिसमें AB = CD और AB || CD है। आइए एक विकर्ण AC खींचें। आप SAS सर्वांगसमता नियम से दर्शा सकते हैं कि
∆ ABC ≅ ∆ CDA है।
इसलिए, BC || AD है। (क्यों?)
आइए अब समांतर चतुर्भुज के इस गुण के प्रयोग के लिए, एक उदाहरण लें।
उदाहरण 6 : ABCD एक समांतर चतुर्भुज है, जिसमें P और Q क्रमश: सम्मुख भुजाओं AB और CD के मध्य-बिंदु हैं (देखिए आकृति 8.18)। यदि AQ, DP को S पर प्रतिच्छेद करे और BQ, CP को R पर प्रतिच्छेद करे, तो दर्शाइए कि:
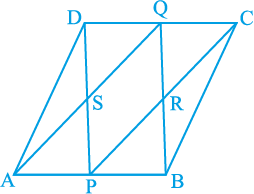
आकृति 8.18
(i) APCQ एक समांतर चतुर्भुज है।
(ii) DPBQ एक समांतर चतुर्भुज है।
(iii) PSQR एक समांतर चतुर्भुज है।
हल : (i) चतुर्भुज APCQ में,
AP || QC (चूँकि AB || CD) (1)
AP = 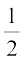 AB, CQ =
AB, CQ = 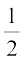 CD (दिया है)
CD (दिया है)
साथ ही, AB = CD (क्यों?)
इसलिए, AP = QC (2)
अत:, APCQ एक समांतर चतुर्भुज है। [ (1) और (2) तथा प्रमेय 8.8 से]
(ii) इसी प्रकार, DPBQ एक समांतर चतुर्भुज है, क्योंकि DQ || PB और DQ = PB है।
(iii) चतुर्भुज PSQR में,
SP || QR (SP, DP का एक भाग है और QR, QB का एक भाग है)
इसी प्रकार, SQ || PR है।
अत:, PSQR एक समांतर चतुर्भुज है।
प्रश्नावली 8.1
1. एक चतुर्भुज के कोण 3 : 5 : 9 : 13 के अनुपात में हैं। इस चतुर्भुज के सभी कोण ज्ञात कीजिए।
2. यदि एक समांतर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइए कि वह एक आयत है।
3. दर्शाइए कि यदि एक चतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करें, तो वह एक समचतुर्भुज होता है।
4. दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
5. दर्शाइए कि यदि एक चतुर्भुज के विकर्ण बराबर हों और परस्पर समद्विभाजित करें, तो वह एक वर्ग होता है।
6. समांतर चतुर्भुज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है (देखिए आकृति 8.19)। दर्शाइए कि
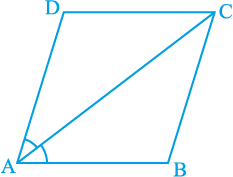
आकृति 8.19
(i) यह ∠ C को भी समद्विभाजित करता है।
(ii) ABCD एक समचतुर्भुज है।
7. ABCD एक समचतुर्भुज है। दर्शाइए कि विकर्ण AC कोणों A और C दोनों को समद्विभाजित करता है तथा विकर्ण BD कोणों B और D दोनों को समद्विभाजित करता है।
8. ABCD एक आयत है जिसमें विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता है। दर्शाइए कि (i) ABCD एक वर्ग है (ii) विकर्ण BD दोनों कोणं B और D को समद्विभाजित करता है
9. समांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिंदु P और Q इस प्रकार स्थित हैं कि DP = BQ है (देखिए आकृति 8.20)। दर्शाइए कि
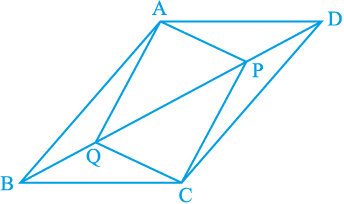
आकृति 8.20
(i) ∆ APD ≅ ∆ CQB
(ii) AP = CQ
(iii) ∆ AQB ≅ ∆ CPD
(iv) AQ = CP
(v) APCQ एक समांतर चतुर्भुज है।
10. ABCD एक समांतर चतुर्भज है तथा AP और CQ शीर्षों A और C से विकर्ण BD पर क्रमश: लम्ब हैं (देखिए आकृति 8.21)। दर्शाइए कि
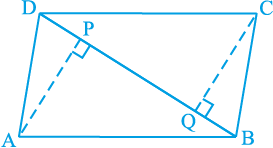
आकृति 8.21
(i) ∆ APB ≅ ∆ CQD
(ii) AP = CQ
11. ∆ ABC और ∆ DEF में, AB = DE, AB || DE, BC = EF और BC || EF है। शीर्षों A, B और C को क्रमश: शीर्षों D, E और F से जोड़ा जाता है (देखिए आकृति 8.22)। दर्शाइए कि
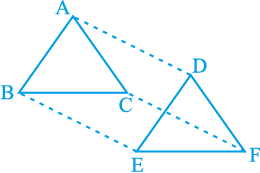
आकृति 8.22
(i) चतुर्भुज ABED एक समांतर चतुर्भुज है।
(ii) चतुर्भुज BEFC एक समांतर चतुर्भुज है।
(iii) AD || CF और AD = CF है।
(iv) चतुर्भुज ACFD एक समांतर चतुर्भुज है।
(v) AC = DF है।
(vi) ∆ ABC ≅ ∆ DEF है।
12. ABCD एक समलंब है, जिसमें AB || DC और AD = BC है (देखिए आकृति 8.23)। दर्शाइए कि
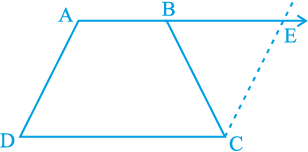
आकृति 8.23
(i) ∠ A = ∠ B
(ii) ∠ C = ∠ D
(iii) ∆ ABC ≅ ∆ BAD
(iv) विकर्ण AC = विकर्ण BD है।
[संकेत : AB को बढ़ाइए और C से होकर DA के समांतर एक रेखा खींचिए जो बढ़ी हुई भुजा AB को E पर प्रतिच्छेद करे।]
8.6 मध्य-बिंदु प्रमेय
आप एक त्रिभुज और एक चतुर्भुज के अनेक गुणों का अध्ययन कर चुके हैं। आइए त्रिभुज के एक अन्य गुण का अध्ययन करें, जो एक त्रिभुज की भुजाओं के मध्य-बिंदुओं से संबंधित है। इसके लिए, निम्नलिखित क्रियाकलाप कीजिए:
एक त्रिभुज ABC खींचिए और उसकी दो भुजाओं AB और AC के मध्य-बिंदु E और F अंकित कीजिए। E और F को मिलाइए (देखिए आकृति 8.24)।
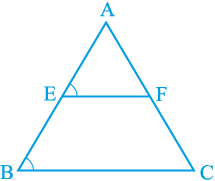
आकृति 8.24
EF और BC को मापिए। साथ ही, ∠ AEF और ∠ ABC को भी मापिए। आप क्या देखते हैं?
आप पाएँगे कि
EF = 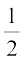 BC और ∠ AEF = ∠ ABC
BC और ∠ AEF = ∠ ABC
है। अत:, EF || BC है।
कुछ अन्य त्रिभुज लेकर, इस क्रियाकलाप को दोहराइए।
इस प्रकार, आप सरलता से निम्न प्रमेय पर पहुँच सकते हैं:
प्रमेय 8.9 : किसी त्रिभुज की किन्ही दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के समांतर होता है।
आप इस प्रमेय को निम्नलिखित संकेत की सहायता से सिद्ध कर सकते हैं।
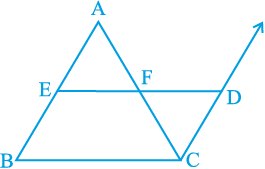
आकृति 8.25
आकृति 8.25 को देखिए, जिसमें E और F क्रमश: ∆ABC की भुजाओं AB और AC के मध्य-बिंदु हैं तथा CD || BA है।
∆ AEF ≅ ∆ CDF (ASA नियम)
इसलिए, EF = DF और BE = AE = DC (क्यों?)
अत:, BCDE एक समांतर चतुर्भुज है। (क्यों?)
इससे EF || BC प्राप्त होता है।
ध्यान दीजिए कि EF = 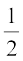 ED =
ED = 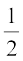 BC है।
BC है।
क्या आप प्रमेय 8.9 का विलोम लिख सकते हैं? क्या यह विलोम सत्य है?
आप देखेंगे कि ऊपर दिए गए प्रमेय का विलोम भी सत्य है। इसे नीचे दिया जा रहा है:
प्रमेय 8.10 : किसी त्रिभुज की एक भुजा के मध्य-बिंदु से दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।
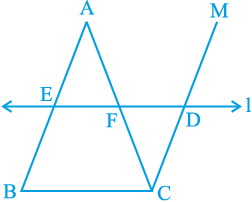
आकृति 8.26
आकृति 8.26 में देखिए कि भुजा AB का मध्य-बिंदु E है और E से होकर जाने वाली रेखा l भुजा BC के समांतर है। साथ ही, CM || BA है।
∆ AEF और ∆ CDF की सर्वांगसमता का प्रयोग करके, AF = CF सिद्ध कीजिए।
उदाहरण 7 : ∆ ABC में, D, E और F क्रमश: भुजाओं AB, BC और CA के मध्य-बिंदु हैं (देखिए आकृति 8.27)। दर्शाइए कि बिन्दुओं D, E और F को मिलाने पर ∆ ABC चार सर्वांगसम त्रिभुजों में विभाजित हो जाता है।
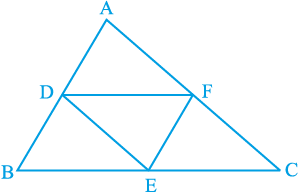
आकृति 8.27
हल : चूँकि D और E क्रमश: भुजाओं AB और BC के मध्य-बिंदु हैं, इसलिए प्रमेय 8.9 द्वारा
DE || AC
इसी प्रकार, DF || BC और EF || AB है।
इसलिए, ADEF, BDFE और DFCE में से प्रत्येक एक समांतर चतुर्भुज है।
अब, DE समांतर चतुर्भुज BDFE का एक विकर्ण है।
इसलिए, ∆ BDE ≅ ∆ FED
इसी प्रकार, ∆ DAF ≅ ∆ FED
और ∆ EFC ≅ ∆ FED
अत:, चारों त्रिभुज सर्वांगसम हैं।
उदाहरण 8 : l, m और n तीन समांतर रेखाएँ हैं, जो तिर्यक रेखाओं p और q द्वारा इस प्रकार प्रतिच्छेदित हैं कि l, m और n रेखा p पर समान अंत: खंड AB और BC काटती हैं (देखिए आकृति 8.28)। दर्शाइए कि l, m और n रेखा q पर भी समान अंत: खंड DE और EF काटती हैं।
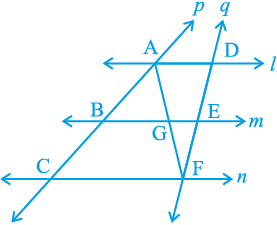
आकृति 8.28
हल : हमें AB = BC दिया है और हमें DE = EF सिद्ध करना है।
आइए A को F से मिलाएँ और इससे AF रेखा m को G पर प्रतिच्छेद करती है।
समलंब ACFD दो त्रिभुजों ACF और AFD में विभाजित हो जाता है।
∆ ACF में यह दिया है कि B, भुजा AC का मध्य-बिंदु है। (AB = BC)
साथ ही, BG || CF (चूँकि m || n है)
अत:, G भुजा AF का मध्य-बिंदु है। (प्रमेय 8.10 द्वारा)
अब, ∆ AFD में भी हम इसी तर्क का प्रयोग कर सकते हैं। क्योंकि G भुजा AF का मध्य-बिंदु है और GE || AD है, इसलिए प्रमेय 8.10 से E भुजा DF का मध्य-बिंदु है।
अर्थात् DE = EF है।
दूसरे शब्दों में, l, m और n तिर्यक रेखा q पर भी बराबर अंत: खंड काटती हैं।
प्रश्नावली 8.2
1. ABCD एक चतुर्भुज है जिसमें P, Q, R और S क्रमश: भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं (देखिए आकृति 8.29)। AC उसका एक विकर्ण है। दर्शाइए कि
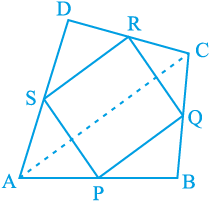
आकृति 8.29
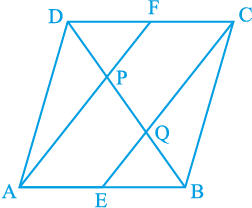
(i) SR || AC और SR = 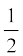 AC है।
AC है।
(ii) PQ = SR है।
(iii) PQRS एक समांतर चतुर्भुज है।
2. ABCD एक समचतुर्भुज है और P, Q, R और S क्रमश: भुजाओं AB, BC, CD और DA के मध्य-बिंदु है। दर्शाइए कि चतुर्भुज PQRS एक आयत है।
3. ABCD एक आयत है, जिसमें P, Q, R और S क्रमश: भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं। दर्शाइए कि चतुर्भुज PQRS एक समचतुर्भुज है।
4. ABCD एक समलंब है, जिसमें AB || DC है। साथ ही, BD एक विकर्ण है और E भुजा AD का मध्य-बिंदु है। E से होकर एक रेखा AB के समांतर खींची गई है, जो BC को F पर प्रतिच्छेद करती है (देखिए आकृति 8.30)। दर्शाइए कि F भुजा BC का मध्य-बिंदु है।
आकृति 8.30
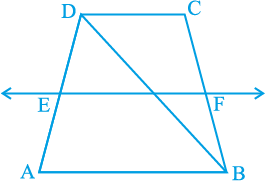
5. एक समांतर चतुर्भुज ABCD में E और F क्रमश: भुजाओं AB और CD के मध्य-बिंदु हैं (देखिए आकृति 8.31)। दर्शाइए कि रेखाखंड AF और EC विकर्ण BD को समत्रिभाजित करते हैं।
आकृति 8.31
6. दर्शाइए कि किसी चतुर्भुज की सम्मुख भुजाओं के मध्य-बिंदुओं को मिलाने वाले रेखाखंड परस्पर समद्विभाजित करते हैं।
7. ABC एक त्रिभुज है जिसका कोण C समकोण है। कर्ण AB के मध्य-बिंदु M से होकर BC के समांतर खींची गई रेखा AC को D पर प्रतिच्छेद करती है। दर्शाइए कि
(i) D भुजा AC का मध्य-बिंदु है। (ii) MD ⊥ AC है।
(iii) CM = MA =  AB है।
AB है।
8.7 सारांश
इस अध्याय में, आपने निम्नलिखित बिंदुओं का अध्ययन किया है :
1. किसी चतुर्भुज के कोणों का योग 360° होता है।
2. समांतर चतुर्भुज का एक विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभाजित करता है।
3. एक समांतर चतुर्भुज में,
(i) सम्मुख भुजाएँ बराबर होती हैं। (ii) सम्मुख कोण बराबर होते हैं। (iii) विकर्ण परस्पर समद्विभाजित करते हैं।
4. एक चतुर्भुज समांतर चतुर्भुज होता है, यदि
(i) सम्मुख भुजाएँ बराबर हों; या (ii) सम्मुख कोण बराबर हों;
या (iii) विकर्ण परस्पर समद्विभाजित करते हों;
या (iv) सम्मुख भुजाओं का एक युग्म बराबर हो और समांतर हो।
5. आयत के विकर्ण परस्पर समद्विभाजित करते हैं और बराबर होते हैं। इसका विलोम भी सत्य है।
6. समचतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं। इसका विलोम भी सत्य है।
7. वर्ग के विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं और बराबर होते हैं। इसका विलोम भी सत्य है।
8. किसी त्रिभुज की किहीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के समांतर होता है और उसका आधा होता है।
9. किसी त्रिभुज की एक भुजा के मध्य-बिंदु से दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।
10. किसी चतुर्भुज की भुजाओं के मध्य-बिंदुओं को एक क्रम से मिलाने वाले रेखाखंडों द्वारा बना चतुर्भुज एक समांतर चतुर्भुज होता है।